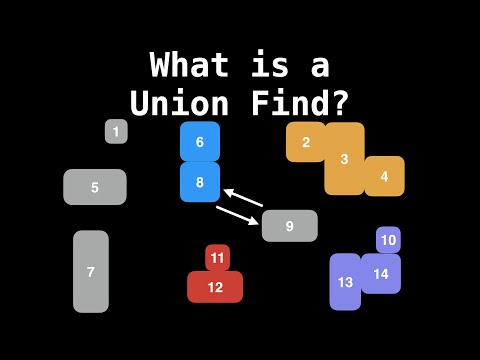
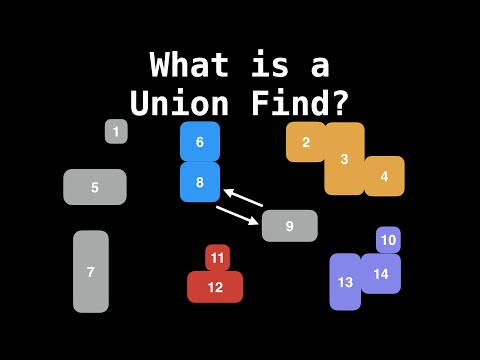
$\huge{\color{Cadetblue}\text{Union find}}$
Union find is a data structure that keeps track of a set of elements partitioned into a number of disjoint subsets. It provides two main operations:
- Find: Determine which subset a particular element is in.
- Union: Join two subsets into a single subset.
The union-find data structure is used to solve problems that involve finding connected components in a graph, such as finding the minimum spanning tree of a graph, or determining whether a graph is connected.
$\Large{\color{darkseagreen}\text{Complexity}}$
| ${\color{cornflowerblue}\text{Operation}}$ |
${\color{cadetblue}\text{Complexity}}$ |
| ${\color{cornflowerblue}\text{Find}}$ |
$\mathcal{O}(\alpha(n))$ |
| ${\color{cornflowerblue}\text{Union}}$ |
$\mathcal{O}(\alpha(n))$ |
where $\alpha(n)$ is the inverse Ackermann function, which grows extremely slowly and is considered to be a constant for all practical purposes. As a result, the time complexity of the find and union operations is effectively $\mathcal{O}(1)$.
$\Large{\color{darkseagreen}\text{Example applications}}$
$\Large{\color{darkseagreen}\text{Playlist}}$